En una distribución normal:
1. La media es mayor que la mediana.
2. La media es menor que la mediana.
3. media y mediana coinciden.
En una distribución normal ¿entre qué puntuaciones típicas se encuentra el 60 % de los casos centrales de la distribución?
1. -0,84 y 0,84
2. - 1,96 y 1,96
3. -1,64 y 1,64
Las puntuaciones de 1000 niños en un test de inteligencia, X, se distribuyen normalmente con media 100 y desviación típica 15. ¿cuál es la probabilidad de obtener puntuaciones menores o iguales que 85?
1. 0,8413
2. 0,1587
3. 0,6826
Las puntuaciones de 1000 niños en un test de inteligencia, X, se distribuyen normalmente con media 100 y desviación típica 15, ¿cuántos niños obtienen puntuaciones superiores a 115?
1. 115
2. 200
3. 159
Las puntuaciones de 1000 niños en un test de inteligencia, X, se distribuyen normalmente con media 100 y desviación típica 15,¿cuál es el Percentil 75 de la distribución?:
1. 110,05
2. 75,00
3. 89,95
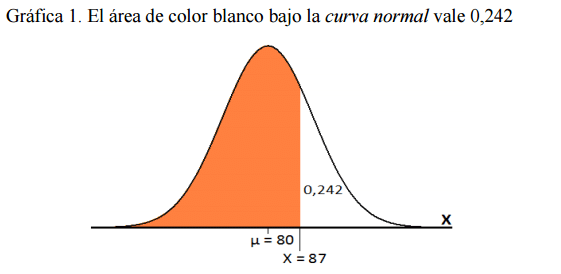
Con la información dada en la Figura 1, ¿cuál es la media de X?:
1. 7
2. 5
3. 6
Con los datos de la Figura 1, ¿cuál es la desviación típica de X?:
1. 3
2. 2
3. 4
Con los datos la Figura 1, ¿cuál será el Percentil 33?
1. 5,24
2. 8,76
3. 5,67
Siguiendo con los datos de la Figura 1, y considerando suspendidos aquellos alumnos que no alcanzan la puntuación 5, ¿cuántos alumnos han suspendido?
1. 250
2. 200
3. 154
Sabiendo que X se distribuye normalmente, que x̄ = 60 y que la puntuación directa 40,8 es superada por el 89,97 % de la distribución, la desviación típica vale:
1. 15
2. 1,28
3. 17,87
Una variable X se distribuye normalmente, con desviación típica 5. Sabiendo que la puntuación 45 deja por encima de sí el 84,13 % de los casos, su media valdrá:
1. 40
2. 50
3. 60
Las puntuaciones de 10000 niños españoles en una prueba de inteligencia (X) se distribuyen normalmente con media 100. Sabemos que 668 niños no alcanzan la puntuación 85 y otros 668 niños obtienen puntuaciones superiores a 115. Su varianza vale:
1. 10
2. 200
3. 100
El 20% de los niños en edad escolar presenta problemas de adaptación al colegio. Si en un determinado centro hay 225 niños, ¿cuál es la probabilidad de que 30 o menos presenten algún problema de adaptación?
1. 0,0080
2. 0,3026
3. 0,0263
El 20% de los niños en edad escolar presenta problemas de adaptación al colegio. Si en un determinado centro hay 225 niños, ¿cuál es la probabilidad de que más de 55 niños presenten algún problema de adaptación?:
1. 0,1040
2. 0,0401
3. 0,4010
El 20% de los niños en edad escolar presenta problemas de adaptación al colegio. Si en un determinado centro hay 225 niños, ¿cuál es la probabilidad de que entre 40 y 50 niños presenten problemas de adaptación?
1. 0,4642
2. 0,2446
3. 0,6424
En una distribución χ² con 28 grados de libertad, el valor 41,34 es:
1. el percentil 5
2. el percentil 90
3. el percentil 95
En una distribución F con 10 grados de libertad en el numerador y 20 grados de libertad en el denominador, ¿cuál es el valor del percentil 90?:
1. 2,20
2. 2,35
3. 1,94
En una distribución F con 10 grados de libertad en el numerador y 20 en el denominador, ¿cuál es el valor del percentil 10?
1. 1,940
2. 2,200
3. 0,454
¿cuál de las siguientes distribuciones NO es simétrica?
1. Normal con media 5 y desviación típica 2.
2. χ² con 10 grados de libertad.
3. t de Student con 10 grados de libertad.
El valor 0,86 se corresponde con:
1. el percentil 80 de una distribución t de Student con 20 grados de libertad.
2. el percentil 5 de una distribución χ² con 19 grados de libertad.
3. el percentil 20 de una distribución t de Student con 20 grados de libertad.
La media y la varianza de las puntuaciones típicas valen, respectivamente, 0 y 1:
1. siempre.
2. nunca.
3. sólo si la distribución es normal.
En una distribución normal tipificada, el percentil 67 vale:
1. 0,44
2. 0,67
3. 0,7486
Se sabe que el absentismo laboral de la empresa se distribuye como una normal de media 2,2 y de varianza 1,44. El percentil 25 es un valor comprendido entre:
1. 0 y 1
2. 1 y 2
3. 2 y 3
En una población, las puntuaciones en un test de memoria se distribuyen normalmente con media 100 y varianza 36. La proporción de sujetos con puntuaciones en el test entre 90 y 110 está entre:
1. 0,10 y 0,15
2. 0,50 y 0,55
3. 0,90 y 0,95
En una distribución normal con media 100 y desviación típica 15, la proporción de sujetos con puntuaciones entre 115 y 85 es igual a:
1. 0,8413
2. 0,1587
3. 0,6826
Las puntuaciones en una prueba de comprensión verbal siguen la distribución normal con media 50 y desviación típica 10. ¿Qué proporción de sujetos obtienen una puntuación superior a 60?:
1. 0,1587
2. 0,5398
3. 0,8413
Sabiendo que las puntuaciones en el test de analogías verbales de la Tabla 1 se distribuyen normalmente, ¿cuál es la proporción de sujetos con puntuaciones entre 22 y 38?:
1. 0,84
2. 0,50
3. 0,68
En una población de 2500 personas, las puntuaciones en un test de inteligencia siguen una distribución normal con media 100 y desviación típica 15. ¿Cuántas personas tienen en el test una puntuación superior a 130?:
1. 15
2. 25
3. 57
Suponiendo que las calificaciones de los 4000 alumnos que se presentaron en la Convocatoria de Febrero al examen de una asignatura se distribuyen normalmente con media igual a 4,7 y desviación típica igual a 3. ¿Cuántos alumnos obtuvieron una calificación igual o menor a 5?
1. 1841
2. 2159
3. 2560
Las puntuaciones en un test de inteligencia siguen una distribución normal de media 100 y desviación típica 15. Si queremos clasificar la población en cuatro grupos de igual tamaño, ¿qué puntuaciones delimitarán estos grupos?
1. 80, 100 y 120
2. 85, 100 y 115
3. 90, 100 y 110
Las puntuaciones en una prueba de psicomotricidad siguen una distribución normal con varianza 9. Si el primer cuartil vale 4, ¿cuál es la media de las puntuaciones en psicomotricidad?
1. 0
2. 1,99
3. 6,01
Respecto a la Gráfica 1, la desviación típica de la distribución de la variable X:
1. vale 1
2. vale 10
3. no se puede calcular
Respecto a la Gráfica 1, la probabilidad de obtener un valor inferior a µ = 80:
1. vale 0
2. vale 0,5
3. no se puede calcular
En una distribución Chi-cuadrado con 7 grados de libertad, el valor 1,239 corresponde al percentil:
1. 1
2. 10
3. 99
Una distribución Chi-cuadrado tiene varianza igual a 32, su media es:
1. 4
2. 16
3. 32
Una variable aleatoria sigue una distribución Chi-cuadrado con varianza igual a 4. Los grados de libertad de esta variable son:
1. 8
2. 2
3. 4
En una distribución Chi-cuadrado con 60 grados de libertad, la P(X > 79,0819) es:
1. 0,05
2. 0,95
3. 0,975
En una variable aleatoria X que sigue la distribución Chi-cuadrado con varianza igual a 40, la probabilidad de que (10,8508 ≤ X ≤ 28,4120) es:
1. 0,95
2. 0,85
3. 0,90
Una variable se distribuye según una t de Student con 20 grados de libertad, ¿cuál es la media de dicha variable?:
1. 20
2. 0
3. hacen falta más datos para calcularla
Respecto a la media de la distribución t de Student:
1. cuanto mayor es el número de grados de libertad mayor es la media.
2. cuanto mayor es el número de grados de libertad menor es la media.
3. no se modifica la media al aumentar los grados de libertad.
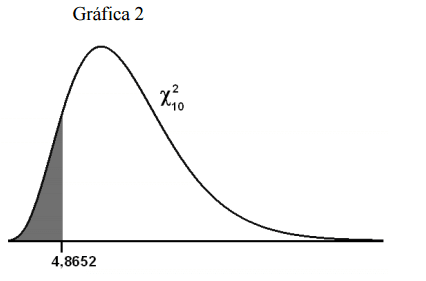
En la Gráfica 2, el área de color gris vale:
1. 0,10
2. 0,50
3. 4,8652
Respecto a la Gráfica 2, ¿cuánto vale la probabilidad de un valor igual o inferior a la media de la distribución?:
1. 0
2. 0,05
3. Todas las opciones son incorrectas
La probabilidad de que una variable X que sigue una distribución t de Student con 10 grados de libertad tome el valor -0,7 o uno menor es:
1. 0,25
2. 0,50
3. 0,75
En las tablas de la t de Student con 16 grados de libertad, el percentil 90 es:
1. 1,337
2. 1,537;
3. 1,737
Las puntuaciones en un test psicomotor se distribuyen según una t de Student con 40 grados de libertad. La probabilidad de obtener puntuaciones mayores que 2,423 es:
1. 0,010
2. 0,005
3. 0,990
Una variable aleatoria se distribuye según la t de Student con varianza igual a 1,20. ¿Cuál es el valor de la distribución que deja por encima al 20% de las observaciones?
1. 0,873
2. 0,849
3. 0,259
En una distribución F de Snedecor con 7 grados de libertad en el numerador y 30 en el denominador, el percentil 5 es:
1. 0,296
2. 2,334
3. 3,376
Una variable X se distribuye según la F de Snedecor con 7 grados de libertad en el numerador y 20 en el denominador. ¿Cuál es el percentil 10 de esa distribución?
1. 2,595
2. 0,385
3. 2,040
La distribución F:
1. es simétrica.
2. puede adoptar cualquier valor entre -∞ y +∞.
3. posee la propiedad recíproca.
¿Cuál de las siguientes distribuciones se emplea habitualmente en pruebas de bondad de ajuste?:
1. Chi-cuadrado
2. F de Snedecor
3. t de Student